The Lagrange multiplier method is undoubtedly the most important method in the optimization theory. But now there is no good online article on the whole method. Therefore, Xiaobian compiled the following article, hoping to win everyone's praise.
The Lagrange Multiplier and KKT conditions are two important methods for obtaining optimization problems with constraints. For the optimization problem of equality constraints, Lagrangian multiplication can be applied. The sub-method is used to obtain the optimal value; if it contains inequality constraints, the KKT condition can be applied to obtain. Of course, the results obtained by these two methods are only necessary conditions, and only in the case of convex functions can be guaranteed to be sufficient and necessary conditions.
The KKT condition is the generalization of the Lagrange multiplier method. When I was learning, I only knew that two methods could be applied directly, but I don't know why the Lagrange Multiplier and KKT conditions can work. Why do you want to find the optimal value? This article will first describe what is the Lagrange Multiplier and KKT conditions; then start to talk about why you should find the optimal value.
I. Lagrange Multiplier and KKT conditions. The optimization problems we usually need to solve are as follows.
:(i) Unconstrained optimization problem, which can be written as: min f(x); (ii) an optimization problem with equality constraints, which can be written as: min f(x), st h_i(x) = 0; i = 1, ..., n (iii) An optimization problem with inequality constraints, which can be written as: min f(x), st g_i(x) <= 0; i =1, ..., nh_j(x) = 0 ; j =1, ..., m For the optimization problem of class (i), the commonly used method is the Fermat theorem, that is, using the derivative of f(x), and then making it zero, the candidate can be found. The figure of merit is then verified in these candidate values; if it is a convex function, it can be guaranteed to be the optimal solution. For the optimization problem of class (ii), the commonly used method is the Lagrange Multiplier, which uses the equality constraint h_i(x) as a formula and f(x). It is called the Lagrangian function and the coefficient is called the Lagrange multiplier. Each variable is derived by the Lagrang function, so that it is zero, the set of candidate values ​​can be obtained, and then the optimal value is verified.
For the optimization problem of class (iii), the commonly used method is the KKT condition. Similarly, we write all the equality and inequality constraints and f(x) as an expression, also called Lagrangian function. The coefficient is also called Lagrange multiplier. Through some conditions, we can find the optimal. A necessary condition for the value, this condition is called the KKT condition.
(a) Lagrange Multiplier For equality constraints, we can combine the equality constraint and the objective function into a formula L(a, x) = f by a Lagrangian coefficient a. x) + a*h(x), where a and h(x) are treated as vector forms, a is the horizontal quantity, and h(x) is the column vector. The reason for this is that csdn is difficult to write mathematical formulas. It can only be used..... Then, the optimal value can be obtained. The L(a, x) can be obtained by taking the zeros and the simultaneous equations. This is said in the higher mathematics, but there is no reason why it can be done. Later, we will briefly introduce its ideas. (b) KKT conditions How do you find the optimal value for an optimization problem with inequality constraints? The commonly used method is the KKT condition. Similarly, all inequality constraints, equality constraints, and objective functions are all written as an expression L(a, b, x)= f(x) + a*g(x)+b *h(x), the KKT condition is that the optimal value must satisfy the following conditions:
1. L(a, b, x) is zero for x; 2. h(x) =0; 3. a*g(x) = 0; after obtaining these three equations, the candidate is the most Excellent value. The third formula is very interesting because g(x)<=0. If you want to satisfy this equation, you must have a=0 or g(x)=0. This is a source of many important properties of SVM, such as support vectors. the concept of.
2. Why are the Lagrange Multiplier and KKT conditions optimal?
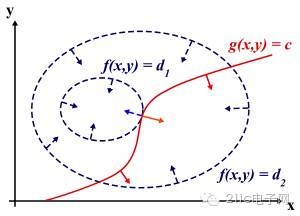
Why do you want to get the best value? Let's first say the Lagrangian multiplier method. Imagine our objective function z = f(x), x is a vector, and z takes a different value, which is equivalent to being projected on the plane (surface) formed by x, that is, the contour is equal. Line, as shown below, the objective function is f(x, y), where x is a scalar and the dashed line is a contour. Now suppose our constraint g(x)=0, x is a vector, on a plane or surface formed by x Is a curve, assuming that g(x) intersects the contour, the intersection is the value of the feasible domain that satisfies both the equality constraint and the objective function, but it is certainly not the optimal value, because the intersection means that there are definitely other contours. The line is inside or outside the contour, making the value of the intersection of the new contour and the objective function larger or smaller, and may be optimal only when the contour is tangent to the curve of the objective function. The value, as shown in the figure below, is that the contour of the contour and the objective function must have the same direction at the normal vector at that point, so the optimal value must satisfy: gradient of f(x) = gradient of a* g(x), a is a constant, indicating that the left and right sides are in the same direction. This equation is the result of L(a,x) deriving the parameters.
The KKT condition is a necessary condition for the optimization problem of the strong dual condition. It can be understood as follows: we require min f(x), L(a, b, x) = f(x) + a*g(x) + b* h(x), a>=0, we can write f(x) as: max_{a,b} L(a,b,x), why? Since h(x)=0, g(x)<=0, now is the maximum value of L(a,b,x), a*g(x) is <=0, so L(a,b,x The maximum value can only be obtained if a*g(x) = 0. Otherwise, the constraint is not satisfied, so max_{a,b} L(a,b,x) is satisfied if the constraint is satisfied. f(x), so our objective function can be written as min_x max_{a,b} L(a,b,x). If we use the dual expression: max_{a,b} min_x L(a,b,x), because our optimization is to satisfy the strong duality (strong duality means that the optimal value of the dual expression is equal to the optimal problem of the original problem) Value), so under the condition that the optimal value x0 is obtained, it satisfies f(x0) = max_{a,b} min_x L(a,b,x) = min_x max_{a,b} L(a,b ,x) =f(x0), let's see what happens in the middle two formulas:
f(x0) = max_{a,b} min_x L(a,b,x) = max_{a,b} min_x f(x) + a*g(x) + b*h(x) = max_{a , b} f(x0)+a*g(x0)+b*h(x0) = f(x0)
It can be seen that the above-mentioned blackening is essentially that min_x f(x) + a*g(x) + b*h(x) has obtained the minimum value at x0, using the fermat theorem, that is, for the function f(x + a*g(x) + b*h(x), find the derivative to be equal to zero, ie the gradient of f(x) + the gradient of a*g(x) + the gradient of b*h(x) = 0
This is the first condition in the kkt condition: L(a, b, x) is zero for x.
As explained before, a*g(x) = 0, then the third condition of the kkt condition, of course, the known condition h(x)=0 must be satisfied, all the above descriptions, the optimization problem that satisfies the strong dual condition The optimal values ​​must satisfy the KKT condition, which is the three conditions described above. The KKT condition can be considered as a generalization of the Lagrangian multiplier method.
Induction Cooker Main Board,Motor Starter Button,Ignition Starter Switch For Foton,Main Spindle Induction Motor
Ningbo Zhenhai Rongda Electrical Appliance Co., Ltd. , https://www.centrifugalswitch.com